Exam 2 Modules 11 to 19
- Due Jul 15, 2024 at 8pm
- Points 18
- Questions 36
- Available Jul 15, 2024 at 6:15pm - Jul 15, 2024 at 8pm 1 hour and 45 minutes
- Time Limit 100 Minutes
Instructions
Copy the following formulas for use during the exam. Make sure to scroll down to see all formulas provided.
Formula for Expected Value is 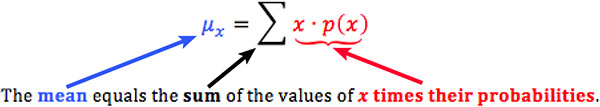
For a normal curve, the Empirical Rule tells us that there is a 68% chance that observations fall within 1 standard deviation of the mean, 95% within 2 standard deviations of the mean, and 99.7% within 3 standard deviations of the mean.
To summarize using probability notation:
These three facts together are called the empirical rule for normal curves.
For quantitative data:
For categorical data:
;
the formula for a confidence interval: Point Estimate+/- Margin of Error ========> p ̂±Zc √((p ̂(1-p ̂))/n)
For our most common confidence levels, the values of Zc are:
- 90% confidence interval: Zc≈ 1.645
- 95% confidence interval: Zc≈ 1.960 (2 is a rough approximation; 1.960 is more accurate)
- 99% confidence interval: Zc≈ 2.576
For the test statistic which is the z-score for the sample proportion. The formula is: